神奈川県 公立高校入試 2022年 倍率分析(志願変更前)
いよいよ倍率が発表されましたね。今年も志願変更に役立つよう、各校の倍率を偏差値順に並べました。私が指導する稲田堤教室と市が尾教室の通学範囲のみです。近くにお住いの方はぜひ参考になさってください。
※対象は下記普通科のみ
●県立(横浜北、横浜中、川崎、相模原学区)
同偏差値の場合は50音順です。

偏差値順にすると、見えてくる傾向があります。
今年目立つのはチャレンジ志向です。
まずは偏差値61以上を見てみましょう。11校中8校倍率が上がりました。昨年よりもチャレンジングで、公立志向と言えます。
この結果を受けて、新城から生田へ、市ヶ尾から港北へ流れる可能性はありますが、チャレンジ志向をはっきり感じるだけに、志願変更が起きづらいように思えます。
次に、偏差値41~44の学校を見てみましょう。応募者減が目立ちます。また、専門科も減っている印象を受けました。つまりこのレベル帯の生徒が専門科に流れたのではないということです。菅ではなく生田東、生田東ではなく百合丘というように、普通科の中でチャレンジ志向が働いたように感じます。
偏差値56~60の層は、複数要因から減ったように思えます。まず、より上位へのチャレンジが起きたことは倍率からも明らかです。また、この偏差値帯にはオール4以上をとれている子が多く、私立推薦をとった可能性もあります。そして、中堅の鶴見、高津などに流れた可能性もあります。このランク帯には、安全志向もトレンドとしてあったと感じます。
一番志願変更が起きそうなのは、倍率が非常に上がった鶴見、高津です。特に、定員がやや少ない高津から、麻生へ志願変更が起こるでしょう。高津狙いの生徒が麻生に移った場合、もともと麻生を志望していた生徒たちは、より一層対策に力を入れる必要があります。こうした点を考慮しつつ、少しずつ倍率が上がっている偏差値46~50の学校でも志願変更が起きるでしょう。しかし、その動きの中でも上矢部、相模田名、菅は埋まりきらないのではないかと思います。
志願変更はすぐに動き始めないと間に合わないタイトなスケジュールですが、しっかり考えて悔いのない選択をしましょう。
最後に、定員割れの学校を志望する方へ、ぜひ勉強を続けてください。過去問にも慣れ、きっと今、伸び盛りのはず。伸びてきた芽をもっと育てられるように、自己ベスト更新に楽しみを見出していってくださいね。
皆様の健闘を心より応援しています。
個太郎塾 稲田堤教室・市が尾教室
北村昌之
休校が子供たちに与えた影響は残っているのか
※本日は保護者の方へ向けた内容です。
昨年の休校は、子供たちの学力にどれほど影響したのでしょうか。その後のハイスピードな授業で、子供たちは理解を深められたのでしょうか。2021年5月27日に全国学力・学習推移調査(以下、状況調査)が行われ、ようやくこの疑問に対する客観的な答えが出されることとなりました。
私は、休校期間の影響は根強く残っていると感じます。状況調査の結果が出るのは4カ月ほど先ですが、期待3割、不安7割の気持ちでいます。
本日は、休校が生んだ学力への影響と、その対応について考えて参ります。この夏の学習計画にお役立て頂けましたら幸いです。

①休校は年齢が低いほど影響があった?
どの学年で影響が大きかったのか、昨年は判断材料がなく、不透明なままでした。
2020年4月に予定されていた状況調査は中止となり、休校が解消された6月以降、状況調査と同規模のテストは行われていませんでした。
しかし、2021年5月、独自に調査を進めていた埼玉県が興味深い資料を発表しました。以下がその資料です。
https://www.pref.saitama.lg.jp/f2214/news/page/news2021051101.html
この調査は、休校を終えた2020年6月から7月にかけて行われました。
埼玉県は、小4から中3に対して
●令和元年度 埼玉県学力・学習状況調査結果データ
●令和2年度 埼玉県学力・学習状況調査結果データ
●臨時休業期間中の児童生徒の学習の保障等のための取組状況調査結果データ
の3つを用いて、休校が学力に及ぼした影響を分析しています。
その結果、以下の点が懸念されました。
●小学生の学力(算数)が下がった可能性がある。
●学力の低下が目立つのは小4・小5である。
●つまり低い学年の方が、影響が大きい。
これはあくまで埼玉県の結果です。しかし、全国的な実態につながっているようにも思えます。学力は基礎から順に積み上げるもの。年齢が低い方が休校に影響されやすいことは言うまでもありません。この調査にない小1から小3への影響も心配されます。
ちなみに、2019年の状況調査で、埼玉県と神奈川県の得点率は63.83%と同値です。神奈川県の生徒にとっては、埼玉県で起きたことは他人事ではありません。
以上から、神奈川県でも、2020年6月には休校の影響があり、その影響は低年齢でより顕著であった可能性が推測されます。
では次に、その影響が現在も残っているのかを考えて参ります。
②影響が残っているかは、結果が出るまで分からない
指導の上では影響の継続を感じます。しかし、状況調査の結果が出るまでは客観的な判断が難しくあります。特に模試の受験者数が少ない小4から中2にかけては「全体の中の位置」が掴みづらくあります。
ただ困ったことに、状況調査の結果を待つと夏休みが終わってしまいます。今年の夏休みは、休校の影響が残っているつもりで、『前年内容から』振り返るべきでしょう。
③夏は経験値も高めたい
以上より、この夏の学習は大変重要です。しかし、学習だけでなく、様々な経験を補うことも大切です。
昨年は部活の大会や遠征が自粛され、合唱、調理実習、体育の一部競技などの実施も見送られた学校がありました。体験や雑学は学びを深める要素です。見たことがない、味わったことがないと、5科の理解もうまく進まないものです。
この夏もまだ、自粛が続くでしょう。何とか生徒たちに経験を積ませたいところです。そこで重要なのが『創作物』です。
読書や映画鑑賞は、様々な疑似体験を与えてくれます。扱われるテーマによっては、漫画でも構いません。教室に通われる皆様には、別途お奨めの本などを紹介して参ります。
④SDGsを知る夏
ここまでは、昨年に目を向け、休校の影響を解消しようという話題でした。
ここからは、将来に目を向け、さらに必要な学びをお伝えします。
近年、入試頻出の題材が『SDGs』です。SDGsをテーマとした英語長文は、大学入試だけでなく、高校入試でも見られ、関連する知識を得ている場合と長文が読みやすくあります。SDGsについて知ることは、いまや入試対策の1つと言えるでしょう。
SDGsに関しては様々な本が刊行されていますが、お勧めできるものは以下の本です。
- 図解SDGs入門
子供から大人まで幅広く読める内容です。グラフを多用しており、日本と各国の現状、取り組みを客観的に把握していくことができます。
ただ、ボリュームがありますので、この本の前に「どのような問題が世界に存在するのか」を映画や漫画を通して知ると良いでしょう。
【まとめ】
●この夏は、2020年3月から学んできた内容の、総復習をお奨めします。
●経験を補う意味合いでも、SDGsを知る意味合いでも、多数の創作物に触れることをお奨めします。
以上、参考となりましたら幸いです。学習のお悩み、ご相談がございましたら、遠方の方でも可能な限り対応をさせて頂きます。どうぞお気軽にご相談ください。
個太郎塾 稲田堤・市が尾教室
北村昌之
学年末の成績が下がってしまった人へ
こんにちは、個太郎塾の北村です。
短かった春休み、まだ気持ちの折り合いがつけられていない人もいるのではないでしょうか。というのも昨年は、1学期の成績が過度に影響してしまった方が全国に多くいる筈なのです。一斉休校となる中で、影響の出なかった人の方が稀かもしれません。2・3学期と挽回していったのに、学年末で1学期の成績が足を引っ張った人、いると思います。学校は、1年の総合評価を学年末の成績とします。3学期で点数がすごく上がったのに、逆に成績が下がってしまった人、きっといますよね。
今日は『頑張ったのに学年末で成績が下がった』人に前を向いてもらうため、当塾での昨年を振り返っていきたいと思います。

・不安が影響した1学期
昨年の一学期は、塾でも対面指導を行えず、顔を合わせて話せなかったことが生徒達にどれほどの不安を与えていたか分かりません。当教室では感染予防を第一に、スクリーニング(来訪)はせず、課題は全て郵送、授業は1:1オンラインで対応していました。最終的にクラスターを出さず1年を終えられましたが、ベストな結果とは思えません。1学期に成績を下げてしまった子がいたからです。
小学生は、学校・友達・習い事が社会との接点です。その3つが一気に遮断された緊急事態は大きなストレスとなったでしょう。また多くの中高生にとって、生活の中心は部活です。学校がいずれ再開されるとしても、今までのように部活はできないだろうと、6月になる前には多くの生徒が覚悟してしまっていました。
不安に耐え、生徒たちは普段の数倍の課題をこなしてくれました。結果、著しく伸びた生徒もいますが、変化に慣れるのに時間がかかった生徒、不安や緊張が理解を妨げた生徒もいました。もっと個別に対応できたのではないか。反省をもとに2学期を迎えることとなりました。
・挽回の2学期
休校期間で成績が下がってしまった生徒は、その差を夏以降に埋めてくれました。対面指導を再開してからの伸びは、目を見張るものがありました。個別指導を頼ってくる生徒には、成績上位者も下位者も、やはり顔を合わせた指導が一番効果的だと実感します。そして、学校再開の安心感もあったことでしょう。リズムよく習得していくことができました。
これは、うちだけで起きたことではないと思います。『夏以降に伸びた』生徒、全国に相当いると思います。これらの生徒たちが、今どういう気持ちになっているか、大部分の生徒が、納得いかない気持ちを抱えているはずです。
・年間総合評価の3学期
夏以降に伸びた生徒、例えば、1学期で平均70点台、成績3をとった生徒がいます。その子は2学期で、中間・期末ともに90点台を取ってくれました。2学期の成績は5です。そして、そのまま3学期でも90点台を獲得してくれました。学年末の成績は4です。
ここまで極端ではなくても、3学期時点では4の実力に至る生徒が、学年総合評価は3になったりする。もし君がそうなら、全く気にする必要はないんです。今、まさに伸び盛りなんです。
「初めから努力しないと結果につながらないんだな」と教訓を得られたなら、それはとても大切なことですが、そう思えた人はきっと稀でしょう。多くの人は「頑張ったのに下がった・・・」と感じてしまったことでしょう。そして勉強量が減ってしまっているんじゃないか。とても心配です。
下がったのは1年間の平均をとったから。君の『今の実力』は『上がっている』んです。下を向く必要はないんです。自分の力をしっかり見定めて、自信を持って今の努力をキープしていけば、今年は必ず成績が上がります。それをしっかりと念頭において、新年度のスタート、ぜひ主体的に、意欲的に取り組んでいってくださいね。
直接指導できる皆さんも、そうでない皆さんも、コロナ禍を乗り越えて頑張ってきた人たち全員、心から応援しています。今年も一年間、頑張っていきましょう。
個太郎塾 市が尾・稲田堤教室
北村昌之
2021年度 高校生模試 日付順年間スケジュール(駿台・河合塾)
こんにちは、個太郎塾の北村です。
高校生の皆さん、模試の計画を立てる時期となりました。
位置を知り、苦手を知り、対策する
そのルーティンを構築するためにも、早くから受験していきましょう。

昨年は感染予防の観点から、会場模試の中止、外部申込の停止が起こりました。
今年も、1種の模試を受け続けることが、必ずできるとは言えない状況です。
複数模試の把握がしやすいよう、駿台模試と河合模試を日程順に並べました。
ぜひ活用してください。
全模試を網羅した表は、多くの先生方が作られると思いますので
自分からは『特に受験人数の多い模試』に絞った表をご提供します。
大学別模試や、東進、代ゼミなどの模試は、別途お調べください。
※変更を確認次第、随時更新します。

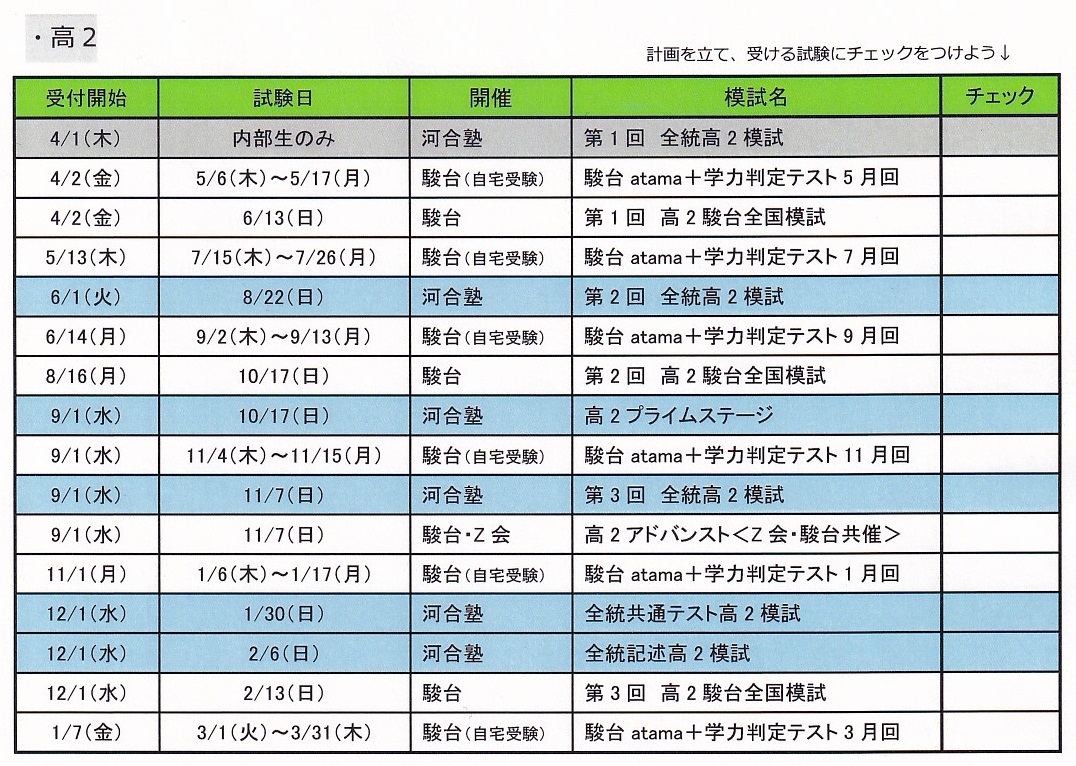

※河合塾、4/1受付開始分の公開会場模試は、一般生の申込不可となっています。
しかし、学校を通した申込(学校が会場)は受け付けているようです。
●判定との向き合い方(高3)
色々な意見があると思いますが、私は年初の判定は気にしないでと言い続けています。
公立と私立で進度差がありますし、当然ながら浪人生は結果が出やすくあります。
夏までは、志望校判定よりも、弱点分析として模試を利用すると良いでしょう。
つまりは自分との勝負です。自己ベスト更新を目指す模試です。
夏以降は、志望校判定や志望校別の順位も意識していきましょう。
ただこの時、悪い判定だから諦めようとなる前に、必ず周りの先生に相談しましょう。
模試は点数による客観的な判定です。
しかし、教えている人にしかわからない主観的な情報があります。
その情報が突破口になる場合もあります。
受験生はよく学ぶとともに、よく相談することが大切です。
●どの模試を受けるべきか
学力、志望校により千差万別です。
周りの先生に相談しましょう。
私からは2つアドバイスさせて頂きます。
1つ目、標準レベルの定着を確かめるうえで『駿台atama+』は大変有効です。
無料で受けられ、日程調整もしやすく、部活と両立しやすい模試です。
ただし、パソコンやタブレットを通した自宅受験です。
紙媒体の模試とは解きやすさが異なることに注意しましょう。
2つ目、国公立志望者は、マーク模試と記述模試をドッキング判定させましょう。
どの模試がドッキング判定できるのか、各模試のサイトで確かめておきましょう。
また、ドッキング判定を希望する人は、日程の被る模試に気をつけましょう。
高3は、第3回全統共通テスト模試とその後の模試とドッキング判定する場合、駿台ベネッセ記述模試が受けられません。
この2つであれば迷いは少ないかもしれませんが、東進なども受ける人は日程の被りに十分気をつけましょう。
●申し込みはすぐ
上記表には、受付開始日しか載せませんでした。
締切日を書いてしまうと、そこまで動かない方が少なからず出てしまうからです。
明日申し込もうと思っている人は、明日も申し込んでいない。
受験に限りませんね。後回しにするのは人間の悪い癖だと思います。
模試の申し込みに限らず、手続き関係は腰を重くしないこと。
思い立ったらすぐ相談、すぐ申し込みという習慣をつけましょう。
受験勉強、本当に大変です。
でも、努力量が一定の水準を超えてくると、本当に楽しくなってきます。
ぜひとも悔いのない受験を。
皆さんの奮闘を心より応援しています。
個太郎塾 市が尾教室・稲田堤教室
北村昌之
何でマイナス×マイナスはプラスなの?
こんにちは、個太郎塾の北村です。
今日は負の数のかけ算、わり算を解説します。
まだ引き算の記事を読んでいない人は、そちらもぜひ読んでくださいね。
マイナスの引き算ってどういうこと? - 個太郎塾 稲田堤教室・市が尾教室のブログ (hatenablog.com)
今回は2ステップで理解しましょう。

ステップ1
かけ算のイメージ
かけ算には物を積むイメージがある。
2×3ならこんな感じだ。

A×Bなら、Bが積む方向を表している。
ここまでは大丈夫かな?
では、思い出してみよう。
皆はかけ算に対して、すでに向きを意識していないかな。
例えば『縦2cm×横3cm』なら、横に積むイメージじゃないかな。

『底面積6cm2×高さ3cm』なら上に積むイメージじゃないかな。

高さのない平面を積むのはおかしな表現だけど
紙を重ねていくと立体になるようなイメージだね。
このような、Bの方向に積むイメージを意識してね。
ステップ2
負の数のかけ算をやってみよう。
先ほどのA×Bをもとにして考えよう。
(+2)×(-3)=(-6)
この場合、Aは(+2)、Bは(-3)だ。
また、『-』は逆方向という意味だったね。
※前回参照
だから、(+2)×(-3)は
(+2)を逆方向に3つ積むイメージだ。
まずは(+2)をイメージして

反対方向にする。

そして、3つ積もう。

どうだろう。イメージ出来てきたかな?
次に、負×負もやってみよう。
(-2)×(-3)=(+6)
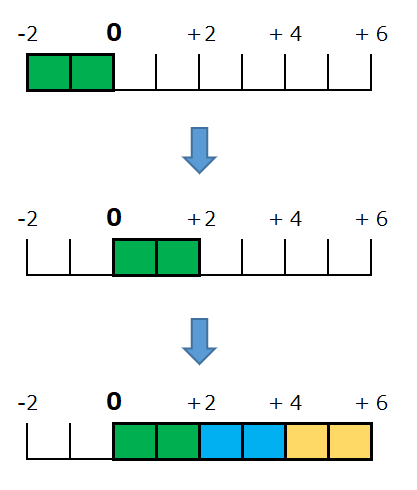
イメージできたかな?
向きが変わる、積まれていく、このような図的なイメージは後々役に立ってくるよ。
補講
負の数のわり算
今回はわり算まで解説するよ。
わり算は、逆数のかけ算に直せる。
だから、かけ算と一緒の考え方でOK。
(-1)÷(-3)は
(-1)×(-⅓)として考えよう。
まずは(-1)をイメージして

それを逆向きに、⅓積むイメージだ。

逆数のかけ算については、改めて解説が必要な人もいるかもしれない。
けど、ひとまずはこのようなイメージだ。
もちろん、公式的に解くのもありだけど、起きていることをイメージできてからにするのがオススメだよ。
正負の計算のイメージを固めよう。
個太郎塾 稲田堤・市が尾教室
北村昌之
マイナスの引き算ってどういうこと?
こんにちは、個太郎塾の北村です。
小6の皆さんはもうすぐ卒業式ですね。
中学の先取りを始めた方も多いのではないでしょうか。
中学数学、難しいですよね。
特に負の数の引き算、多くの人が混乱します。
今日はその『負の数の引き算』を
3ステップで理解しましょう。

※ここからは授業のように進めます。
●ステップ1
正負の数は方向を持つ。
まず、正負の数を理解しよう。
正負の数は、向きを持った数だ。
『+』の方向を決めたら、『-』が逆方向。
図で表すとこんな感じだ。

正の方向を決めたら、その逆が負の方向。
ななめでも同じです。
まずはこれを覚えてね。
●ステップ2
引き算ってどういう計算?
例えば、5-3は
5と3の差を求める計算だ。
数直線で表すと、点線のところが差だ。

答えは2。
じゃあ、皆、この『2』を今までどんな風に見ていたかな?
次の①~③から選んでみてね。

算数ではどれも正解かもしれないけど、これが正負の数で表した(+5)−(+3)という式であったら、②が正解なんだ。
正負の数は『向きを持つ数』だから、答えの方向も、はっきり決めなきゃいけないんだ。
じゃあ、どうやって方向を決めるのか、一緒に考えていこうね。
引き算を言葉でとらえてみよう。
5は3よりどれだけ大きいか。
『より』って言葉に注目だ。
この言葉を使ったら、AとB、どっちが基準かな?
AはBより背が高い。
Bから見て、Aの方が、背が高い。
Bが基準だね。
つまり
Bから見たAの方向が、答えの方向だ。
●ステップ3
負の数の引き算をやってみよう
(+5)-(-3)= ?
まずは、正-負から考えていくよ。
Aさんが(+5)の位置、Bさんが(-3)の位置にいると考えよう。

Bさんから見て、Aさんは+の方向に8進んだ位置にいるよね。
だから、答えは+8になる。
次に、負-負をやってみよう。
(-5)-(-3)= ?
Aさんが(-5)の位置、Bさんが(-3)の位置にいると考えよう。

Bさんから見て、Aさんは-の方向に2進んだ位置にいる。
答えは-2。
どうだろう。イメージ出来たかな?
引き算は差を求める計算。
中学では、そこに向きが加わっただけなんだ。
最後に、ポイントを整理しよう。
・正負の数は、向きを持つ数
・A-Bは、B視点で方向を決める
・慣れるまでは数直線を書く
慣れてきたら公式的に解いても問題なし。
でも、最初から公式だけでクリアするのは危険だ。
学習は土台が最も大切。
起きていることをイメージできるようにしよう。
次回は『負のかけ算』を一緒に勉強しよう。
個太郎塾 稲田堤・市が尾教室
北村昌之
英単語の覚え方が分かりません!
英単語ってどう覚えればいいの?
今年、最も多く受けた質問です。
先生からのアドバイス
『認識の仕方』を変えよう。
それだけでかなり改善されます。

皆は「校」って漢字をどう認識しているかな?
多分、「木+交」じゃないかな?
パーツを認識できるから、記憶に残っていく。
英単語をパーツに分ける意識を持とう。
さらに、ローマ字分けをしないように。
例えば「page」を「pa/ge」と分けている人は「p/age」に変えよう。
カタカナ表記で申し訳ないですが、「age」は「エイジ」と読みます。
「プ+エイジ=ペイジ」です。
では次に、「start」も考えてみよう。
これは「st/art」と分けるのが良いと思います。
「st(ストゥ)」に「art(アート)」をつけて「start(スタート)」。
発音の塊を覚えると、その組み合わせで単語暗記が進むようになる。
暗記効率がぐっと上がります。
図にするとこんな感じ。

「age」と「st」を覚えていたら、新しく覚えるところ、すごく少なくなることが分かるでしょう。
成績が高い子でもローマ字読みで暗記している場合は多いです。
でも、ローマ字暗記はいつか壁に当たる時が来てしまう。
矯正は大変だけど、本格的に直したい人はフォニックスからしっかり学び直そう。
今年から、英単語の暗記量は1.5倍。
努力では乗り切れない個数。
暗記の効率を高めて負担を減らしていこう。
個太郎塾稲田堤教室・市が尾教室
北村昌之